Méthodologie

LA MÉTHODE DES ABAQUES

La méthode des Abaques, élaborée à partir des écrits des auteurs constructivistes, Piaget et Wygotski, vient de trouver une confirmation et une validation à la suite de la découverte de Fahrenfort (2012) : la stabilité dans les apprentissages fondamentaux est essentielle.

 

• Un modèle Constructiviste TGR

La première étape, la Transition, permet de construire la notion ou le concept à partir d’un exemple, d’un cas particulier. C’est un apport de Piaget.
La deuxième étape, la Généralisation, consiste à définir une catégorie qui regroupera dans une même notion ou concept l’ensemble des particularités envisagées. C’est un apport de Piaget.
La troisième étape, la Représentation, est une image mentale technique définitive qui permettra de mémoriser sur le long terme la notion ou le concept. C’est un apport de Wygotski.

 

• En mathématiques, les outils

Ces outils, au nombre de trois, permettent de construire l’ensemble des notions fondamentales (jusqu’à la fin du collège, au moins). Ils sont nécessaires et suffisants.
Le boulier didactique autorise la construction du système de numération positionnelle décimale à partir des seules bases trois et cinq reconnues par le cerveau humain.
Le tableau [Partie-Partie-Tout] permet la compréhension de toutes les situations additives.
Le tableau [Règle de trois] permet la compréhension de toutes les situations multiplicatives.

Constructivisme et boulier didactique

 

• L’histoire pour éclairer obstacles et innovations d’aujourd’hui

Avec le livre « Méthode des Abaques »

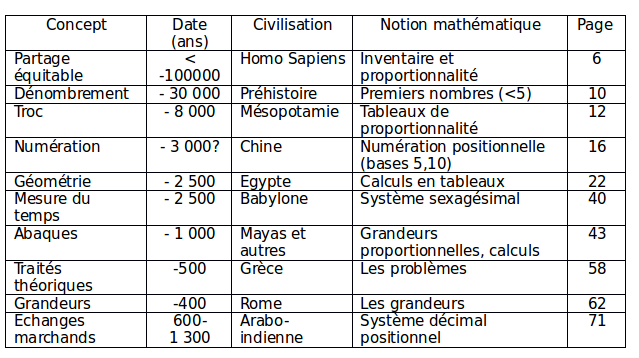
Pour comprendre cette nouvelle approche du calcul, l’éclairage de l’Histoire et de l’apparition des notions mathématiques, est indispensable. Ce voyage dans le temps est proposé en 10 planches de bandes dessinées qui découpent en séquences les 80 pages de cours illustré. L’ensemble du programme de l’école primaire est ainsi découvert ou redécouvert.

 

• Définitions proposées pour les mots clés :

Abaques : Tables de calcul, incluant les bouliers, les tableurs informatiques, les tableaux sur papier en général, les tables numériques, les familles de courbe, etc.

Calcul : Mise en relation des quantités, directement à partir de leurs représentations numériques.

Dyscalculie : Dysfonctionnement ou trouble d’origine neurologique chez certains sujets entraînant des difficultés en calcul.

Innumérisme : Situation, susceptible d’évolution, des sujets dont la numératie est insuffisante.

Math : Abréviation (donc sans ‘s’) de la Mathématique ou des Mathématiques ; la forme apocopée Maths est aussi souvent utilisée.

Numératie : Ensemble des connaissances et compétences de base requises pour conduire un calcul.

Notion : Terme spécifique désignant un concept en mathématiques.

 

 

LE BOULIER DIDACTIQUE

• Un outil généralisateur

La base cinq et la base 10

La représentation du nombre s’effectue avec les doigts jusqu’à dix.
(voir « Méthode des abaques » page 11, 17 et 21)
Et ensuite ?
Dans l’apprentissage du langage, les concepts ont habituellement une image ; ainsi lorsque l’on dit « cheval », on voit le mot mais aussi la tête du cheval. Une rose, c’est une fleur que l’on peut se représenter.
Or, nous savons que seules les trois premières quantités, nombre de barres par exemple (une, deux et trois), ont une représentation mentale possible.
Apprendre que huit c’est le symbole 8, sans aucune possibilité de représentation mentale, c’est comme si nous voulions faire comprendre à un enfant que la philosophie, c’est la lettre grecque φ.
Heureusement pour les 10 premiers nombres, il y a les doigts, en base cinq, mais ensuite,
Ensuite quel est l’outil ? Une représentation au tableau, l’abaque à colonnes, les bûchettes ? Autant d’outils que de classes. Les outils généralisateurs, par excellence, sont les bouliers, héritiers de l’abaque romain en base cinq.
Il est prouvé que la représentation mentale des 10 premiers nombres s’effectue en base trois en utilisant, aussi, les compléments à cinq.

*Huit, ce n’est pas 8 doigts mais bien 1 main et 3 doigts

*L’écriture romaine est bien VIII

*Certaines tribus d’Océanie ou d’Amazonie savent compter jusqu’à 5 seulement (un, deux, trois, beaucoup, ‘très’ beaucoup)

*Les nombres jusqu’à trois sont ’spontanés’ et reconnus par des bébés de quelques mois

Le boulier didactique permet de construire la numération en utilisant un maximum de 3 perles, facilement représentables (perles unaires activées ou leur complément à cinq, perles quinaires activées). Ainsi n’importe quel nombre peut avoir une image mentale bien plus représentative de la quantité correspondante que le nombre écrit avec les symboles arabo-indiens.
Le boulier est le seul outil qui permet de développer la mémorisation déclarative (par cœur) et la mémorisation procédurale (construction par le calcul mental) des tables d’addition et des tables de multiplication.

 

 

•  Les mauvais choix de la révolution

  

L’interdiction de l’utilisation des abaques à l’école

La lutte entre les abacistes, héritiers des clercs de l’Eglise qui détenaient un monopôle sur le calcul avec les abaques et les chiffres romains, et les algoristes qui privilégiaient les algorithmes et les chiffres arabes, s’est conclue par l’interdiction de l’abaque, trop lié à l’Eglise, lors de la Révolution.

Nous savons maintenant que la majorité des élèves ont besoin d’une représentation concrète pour se faire une image mentale.
L’utilisation du sens du toucher et des couleurs consolide la représentation mentale et la fixe.

La mort de Condorcet en prison en 1794

Il n’aura pas eu le temps de défendre son système plus simple, qui limite à dix les nombres de base pour une bonne logique de la construction de la numération (nous utilisons vingt nombres de base dans le système officiel avec des irrégularités de surcroît : Onze, douze, treize, quatorze, quinze, seize, vingt, soixante-dix, quatre-vingt, quatre-vingt-dix). Cette exception nationale, c’est beaucoup de temps perdu (deux ans de retard pour tous les écoliers francophones par rapport à l’ensemble des pays, notamment asiatiques ?).
Quoi de plus simple que dix-un, dix-deux, dix-trois, dix-quatre, dix-cinq, dix-six, dix-sept, … duante, trente, … septante, huitante, nonante ? Cela éviterait le supplice, pour le maître, aussi bien que pour l’écolier, de l’apprentissage de ces irrégularités en CP.

 

• Le boulier didactique

C’est le prolongement des mains !

 

 

LES APPORTS DES CONSTRUCTIVISTES

Le modèle TGR de construction des apprentissages est directement issu des réflexions des auteurs constructivistes ; les étapes de Transition et de Généralisation ont été définies par Piaget qui n’a, semble-t-il, pas noté l’importance de l’étape de Représentation, décrite par Bruner mais surtout par Wygotski

 

• Que disent les auteurs constructivistes ?

Piaget écrit, par exemple, au sujet du cheminement mental vers la notion de la multiplication ?
« Si nous retrouvons, sous des présentations aussi bénignes, les difficultés habituelles de la multiplication, nous pouvons espérer parvenir à dégager leurs raisons et du même coup les conditions d’abstraction réfléchissante rendant la multiplication utilisable et compréhensive. » (Piaget, 1977, p32)
« Le premier stade montre déjà de façon claire la différence entre l’addition, où la pensée est centrée sur les objets que l’on réunit à d’autres, donc sur le résultat de cette réunion, et la multiplication où il s’agit en plus de dégager le nombre de fois qu’on les réunit donc de dénombrer les opérations comme telles et non plus seulement leurs résultats en tant que nombre des objets transférés. »1 (Piaget, 1977, p32)

Effectivement, l’addition fonctionne bien, les tableaux fonctionnent bien. Pourquoi ? Ainsi que le dit Piaget, dans le cas de l’addition, la pensée est centrée sur un seul sujet (la réunion d’éléments identiques). Dans le cas de la multiplication il y a deux sujets à suivre pour faire la réunion de tous les éléments, la cardinalité de l’ensemble de départ et le nombre de fois qu’il faudra le prendre. En mathématiques, nous parlons de loi de composition interne ou externe.

La pensée ne peut pas facilement suivre et ‘contrôler’ ces deux sujets à la fois ce qui est conforme aux modèles de Vygotski (p 54, 417) ou de Bruner (p 193), qui parlent bien, respectivement, d’une seule « unité de base » ou d’un seul « prototype » pour amorcer le raisonnement.

Les tableaux, avec une entrée (addition) ou deux entrées (multiplication) forment un tout comme l’eau que l’on ne peut pas décomposer en ses «éléments constitutifs (H2 + O2) » sans en changer totalement les propriétés, suivant l’exemple de Vygotski (p 51). Les tableaux sont donc nos « unités de base » à partir desquelles le raisonnement pourra se développer dans une seule direction. Nous utiliserons aussi l’expression, « image mentale prototype multi-sensorielle » ou plus simplement, « image mentale »

 

• L’Abstraction Réfléchissante de Jean Piaget

Que dit Piaget des apprentissages mathématiques (*) ?

Il est tout d’abord surpris, comme nous le sommes, en découvrant certaines difficultés (il y a plus de 50 ans…).
« Nous pensons aux difficultés surprenantes de l’enfant à comprendre la signification des multiplications ultrasimples. » (Piaget, p 7)
« Avec le stade de 11-12 ans qui est celui de la pensée formelle, donc des abstractions sur les abstractions ou de la réflexion à la nième puissance, le sujet trouve enfin les solutions… On est surpris qu’il faille attendre ce niveau d’âge pour des raisonnements aussi simples. » (Piaget, p24)
« Reste alors à expliquer une telle myopie à l’égard de structures multiplicatives aussi simples et même transparentes. » (Piaget, p35)
Il propose ensuite une démarche cognitive ‘l’abstraction réfléchissante’ pour les apprentissages logico-arithmétiques : Deux étapes qu’il oppose à ‘l’abstraction empirique’ pour les concepts quotidiens :
« En premier lieu elle transpose sur un plan supérieur ce qu’elle emprunte au palier précédent (par exemple en conceptualisant une action) et nous désignerons ce transfert ou cette projection sous le terme de « réfléchissement ». En second lieu elle doit alors nécessairement reconstruire sur le nouveau plan B ce qui est tiré de celui de départ A, ou mettre en relation les éléments extraits de A avec ceux déjà situés en B: Cette réorganisation obligée par le réfléchissement sera dite « Réflexion ». » (Piaget, p 6)
La ‘Réflexion’ est aussi définie comme « la réorganisation d’un nouveau tout »

 

Comment interpréter la pensée de Piaget ?

Nous représentons le modèle proposé pour les abstractions logico-arithmétiques par une échelle dont la progression de barreau en barreau s’effectue ainsi :
Prenant appui sur l’un des barreaux, l’on peut atteindre le barreau au-dessus (Réfléchissement ou Différenciation).
A ce moment-là le poids du corps repose sur le nouveau barreau (Réflexion ou Généralisation) ce qui permettra une nouvelle progression.

Ce modèle imagé permet de comprendre la progression en mathématiques. La progression doit être verticale, l’assimilation de chaque concept étant indispensable pour aborder le suivant ; ainsi, si le concept ‘multiplication’ n’est pas assimilé, la progression sur l’échelle logico-arithmétique est donc bloquée. On ne peut en sauter un barreau !

Références :
* Piaget (J), Recherches sur l’abstraction réfléchissante: 1/L’abstraction des relations logico-arithmétiques. Paris: PUF, 1977.

 

• L’image mentale prototype de Jérôme Bruner

« … Des trois modes de représentation , décrits par Bruner, le mode ‘énactif’ (les actions), le mode ‘iconique’ (les images) et le mode ‘symbolique’ (le langage) qui prennent plus ou moins d’importance et s’articulent différemment et de façon complémentaire suivant les périodes de la vie (figure 2b), il faut reconnaître que le mode ‘symbolique’, c’est à dire l’approche verbale par le langage écrit ou oral est adoptée préférentiellement dans notre enseignement des mathématiques depuis des décennies. Mais cette présentation ne convient plus à un très grand nombre d’écoliers ou d’élèves, comme nous l’avons vu précédemment (Innumérisme, ‘Constats’, pages 6 et 7). Nous préférons privilégier les deux autres modes ‘énactif’ et ‘iconique’ en conservant le minimum du mode ‘symbolique’, ce qui aboutit en fait à travailler dans la partie colorée en jaune du schéma (figure 2b, p 12). Ce choix, avec les outils proposés à nos élèves en difficulté de 7 à 16 ans, aboutit à la formation d’une image que nous avons choisi d’appeler « image mentale ». Elle va nous servir de concept « prototype » pour des développements et raisonnements ultérieurs. J. Piaget avec « l’abstraction empirique » semble décrire, sinon le même mode de représentation .

 

• L’Unité de Base de Lev Semionovitch Vygotski

« … Mais Vygotski étudie ensuite les concepts scientifiques en distinguant les « concepts quotidiens » issus de l’expérience (pensée technique) et les « concepts scientifiques » introduits par l’apprentissage scolaire. Il introduit, comme vu précédemment (page 10), la notion d’unité de base du concept, «edinica » en russe; comme l’eau, « qui éteint le feu», et que l’on décomposerait en Hydrogène et en Oxygène (mélange explosif), cette unité de base est un « tout » que l’on ne peut diviser sans prendre le risque de changer ses propriétés. Dans cette expressionplus général de ‘représentation mentale multi-sensorielle’ où le toucher, notamment, a sa place.
Notons, aussi, que la ZPD est bien la Zone Prochaine de Développement. Le terme « proximal » ne correspond pas à la pensée de Vygotski que F. Sève a plus justement traduit « prochaine ». Le modèle d’apprentissage représente, ainsi, une construction de proche en proche que Piaget, dans son « abstraction réfléchissante », n’aurait pas reniée, s’il avait connu les écrits de l’auteur russe censuré par Staline. Il le dit, d’ailleurs, dans un commentaire publié en appendice de la traduction de l’ouvrage de Vygotsky, en 1997

Notre modèle constructiviste est ainsi mis en place.

 

LES APPORTS DES NEUROSCIENCES

• Que répond la science aujourd’hui ?

La difficulté de suivre deux sujets, comme le remarque Piaget, est aujourd’hui bien expliquée. Etienne Koechlin montre expérimentalement que le cerveau fonctionne en monotâche. Par ses conséquences dans la vie de tous les jours, cette découverte scientifique est de la plus grande importance et va modifier notre ‘environnement machines’; le téléphone au volant en est une illustration bien connue. Les fabricants d’avion envisagent aussi un récapitulatif visuel des informations de vol essentielles, sur un écran (primary flight display), pour contrer le phénomène de « tunnellisation » ou « persévération », qui en cas de stress, empêche l’utilisation des procédures habituelles, ce qui semble à l’origine d’accidents récents. Cette découverte confirme ainsi le bien-fondé de notre approche par le tableau qui est un ‘récapitulatif visuel’ d’un énoncé verbal difficile à déchiffrer par une procédure mentale longue qui n’est pas à la portée de tous. Nous démontrons ainsi qu’un énoncé de deux lignes aboutissant à une multiplication, à une division ou à un calcul de proportionnalité c’est 23 étapes d’abstraction et 864 solutions de calcul possibles. Laisser à l’intuition mathématique ou à l’application d’une procédure inutilisable, car trop longue, surtout en cas de stress, conduit très souvent à l’échec les élèves et même les ministres de l’Education Nationale, bac + 5 ou bac +7. Il est remarquable que nos trois auteurs constructivistes du siècle dernier aient anticipé à ce point les solutions que les découvertes récentes vont imposer dans l’enseignement de la mathématique à très court terme.
D’autres découvertes orientent notre méthodologie ; notons ces avancées récentes qui sont étudiées dans le document joint Les neurosciences et les maths

 

*Processus de concentration avant la prise de conscience (Dehaene, Le code de la pensée, 2014)
*Dans le doute la conscience s’abstient, ou la stabilité des apprentissages (J. Fahrenfort, 2013)
*Le système exécutif doit inhiber l’intuition au profit du raisonnement (O. Houdé, 2014)
*Le cerveau est monotâche (E. Koechlin 2010)
*Le cerveau fonctionne souvent en mode automatique (M. Raichle, 2011)
*Le cerveau fonctionne aussi en mode par défaut (A. Destexhe, 2013)